A collection of example kernels implemented using the Triton language and explanations of how they work.
Triton Example Kernels
向量加法
向量加法是最简单的并行计算模式之一, 它将两个向量的对应元素相加。以下是一个使用 Triton 实现的向量加法内核示例:
import torch
import triton
import triton.language as tl
@triton.jit
def add_kernel(x_ptr, y_ptr, output_ptr, n_elems, BLOCK_SIZE: tl.constexpr):
pid = tl.program_id(0)
block_start = pid * BLOCK_SIZE
# generate a 1D range of offsets for the current block
offsets = block_start + tl.arange(0, BLOCK_SIZE)
mask = offsets < n_elems
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
tl.store(output_ptr + offsets, output, mask=mask)
def add(x: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
assert x.shape == y.shape
n_elems = x.numel()
output = torch.empty_like(x)
BLOCK_SIZE = 1024
grid = lambda meta: (triton.cdiv(n_elems, meta['BLOCK_SIZE']),)
add_kernel[grid](x, y, output, n_elems, BLOCK_SIZE=BLOCK_SIZE)
return output这个例子用来展示 Triton 的基本语法. 对于一个 Triton 内核, 用 @triton.jit 装饰器进行标记, 装饰后的函数会被编译成 GPU 代码, 它可以通过在调用时加上 [] 来指定 Grid Size. 例如 add_kernel[grid](...).
Grid Size 的定义通常是一个 Lambda 函数, 它接受一个 meta 字典, 它包含了内核中定义的所有 tl.constexpr 参数, 可以通过从 meta 中动态获取这些参数来计算对应的 Grid Size. 这么做的是为了 @triton.autotune 服务的, 自动调优的时候经常修改例如 BLOCK_SIZE 这类参数, 通过 meta 来获取最新的参数值能够保证 Grid Size 的正确性.
tl.program_id() 用来相当于 blockIdx, 里面用索引表示要获取的块索引的维度, 例如 tl.program_id(0) 获取第 0 维的块索引.
通常使用 mask 来处理边界条件, 配合上 other 参数用来处理越界访问的情况, 例如 tl.load(x_ptrs, mask=mask, other=0.0).
接着是一个 Benchmark 的使用示例, 用来对比 Triton 内核和 PyTorch 内置操作的性能:
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['size'], # x axis name
x_vals=[2**i for i in range(10, 28)], # x axis values
x_log=True, # enable log scale for x axis
line_arg='provider', # argument name to distinguish lines
line_vals=['triton', 'torch'],
line_names=['Triton', 'PyTorch'],
styles=[('blue', '-'), ('green', '--')],
ylabel='GB/s',
plot_name='vec-add-perf',
args={},
)
)
def benchmark(size, provider):
x = torch.randn(size, device='cuda', dtype=torch.float32)
y = torch.randn(size, device='cuda', dtype=torch.float32)
quantiles = [0.5, 0.2, 0.8]
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: add(x, y), quantiles=quantiles)
else:
ms, min_ms, max_ms = triton.testing.do_bench(lambda: x + y, quantiles=quantiles)
gbps = lambda ms: 3 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3)
return gbps(ms), gbps(min_ms), gbps(max_ms)
benchmark.run(print_data=True, show_plots=True)Triton 提供了 testing.perf_report 装饰器来方便地进行性能测试和结果可视化. x_names 和 x_vals 定义了横轴的名称和取值, 它会以 kwarg 的形式被传递给被装饰的函数, 因此名称必须匹配. line_arg 定义了用来区分不同测试线的参数名称, 同样会以 kwarg 的形式传递给被装饰的函数.
通过 testing.do_bench 来运行基准测试, 它接受一个 Lambda 函数作为被测试的代码块, 还有一个 quantiles 参数用来指定要计算的延迟分位数. 例如 [0.5, 0.2, 0.8] 分别表示总延迟的中位数, 20% 分位数和 80% 分位数, 因此返回的第二个结果是最优延迟, 第三个结果是最差延迟.
最后对于向量加法的性能, 可以选择通过计算内存带宽来衡量, 公式为 3 * N * elem_size / time, 其中 N 是向量的元素数量, 3 因为处理一个输出元素需要两次读取一次写入.
Fused Softmax
用 Triton 可以很方便实现 Softmax 中的算子融合 (融合交给编译器完成), 减少昂贵的内存读写操作.
import torch
import triton
import triton.language as tl
@triton.jit
def softmax_kernel(i_ptr, o_ptr, i_stride, o_stride, n_rows, n_cols, BLOCK_SIZE: tl.constexpr, num_stages: tl.constexpr):
row_start = tl.program_id(0)
row_step = tl.num_programs(0)
for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
row_start_ptr = i_ptr + row_idx * i_stride
col_offsets = tl.arange(0, BLOCK_SIZE)
i_ptrs = row_start_ptr + col_offsets
mask = col_offsets < n_cols
x = tl.load(i_ptrs, mask=mask, other=-float('inf'))
x_minus_max = x - tl.max(x, axis=0)
exp_x = tl.exp(x_minus_max)
sum_exp_x = tl.sum(exp_x, axis=0)
softmax = exp_x / sum_exp_x
o_ptrs = o_ptr + row_idx * o_stride + col_offsets
tl.store(o_ptrs, softmax, mask=mask)每个 Block 处理输入矩阵中的一行的数据. 首先通过 tl.program_id(0) 获取当前 Block 初始时要处理第几行, 而 tl.num_programs(0) 则表示总共有多少个 Block, 也就是迭代的步长. 通过 tl.range 生成每个 Block 需要处理的所有行的索引.
接着计算当前行的起始指针, 同样通过 tl.arange 生成一个 1D 的列偏移量数组. 需要注意的是, 不能假定数据在内存中是紧凑连续储存的, 即使大多数情况下整块数据在内存中连续, 但如果对其切片后传入内核, 那数据就不再是连续的了, 例如将 [100, 100] 的张量切片成 [:, 50], 那么每行数据在内存中就是隔着 100 个元素存储的, 但同一行的数据仍然是连续的. 因此需要通过传入的 i_stride 和 o_stride 来计算每行数据的实际起始地址.
接着同样使用 mask 和 other 参数来处理边界条件, 避免越界访问. 然后按照 Softmax 的计算步骤依次进行计算, 最后将结果存储回输出指针处. 很显然通过 Triton, 编译器帮忙处理好了 Reduction 的问题, 实际上归约操作不好优化, 涉及到对齐和线程间通信, 片上内存容量等问题.
但这个内核实际上有一个约束, BLOCK_SIZE 必须大于等于 n_cols, 否则一个 Block 处理不完一行数据, 结果就是错误的.
矩阵乘法
矩阵乘法应该是最重要, 也是最基础的并行计算模式了, 但是优化起来其实非常复杂, 首先它既有逐元素计算的部分, 也有归约的部分, 其次它涉及到二维数据的访问和储存, 还有数据在内存中的布局问题 (行优先 v.s. 列优先), 以及如何利用片上内存 (Shared Memory) 来提升数据重用率等问题. 下面是 Triton Tutorial 中的例子, 首先解释一下 Super-group 的优化方式.
传统的 Row-Major 矩阵乘法中, 每个 Block 可能负责计算结果矩阵 中的一行, 例如为了计算结果的第一行, 需要加载矩阵 的第一行和矩阵 的所有列, 计算完后存储回结果矩阵 的第一行. 当 矩阵很大时, 显然 GPU L2 缓存不一定存得下整个 矩阵, 会把 矩阵的行数据从 L2 中挤掉, 而 的数据是要被频繁复用的, 最后的结果就是 L2 命中率下降, 性能下降.
因此一种用来提升 L2 命中率的方法是, 将多个 Block 组成一个 Super-group (超级组), 让同一个超级组内的 Block 负责计算结果矩阵 中相邻的多行数据. 具体的步骤如下:
- 分组: 将结果矩阵 沿着列方向划分成若干个组, 每个组中包含
GROUP_SIZE_M个 Block. - 重排: 在每个组内, 沿着列方向依次分配 Block 计算任务, 这样同一个组内的 Block 会计算结果矩阵 中相邻的多行数据.
下图直观展示了效果, Row-Major 的做法是每个 Block 计算结果矩阵 中的一行数据, 而 Super-group 的做法是每个组计算结果矩阵 中的一块数据, 组内的 Block 计算相邻的多行数据.
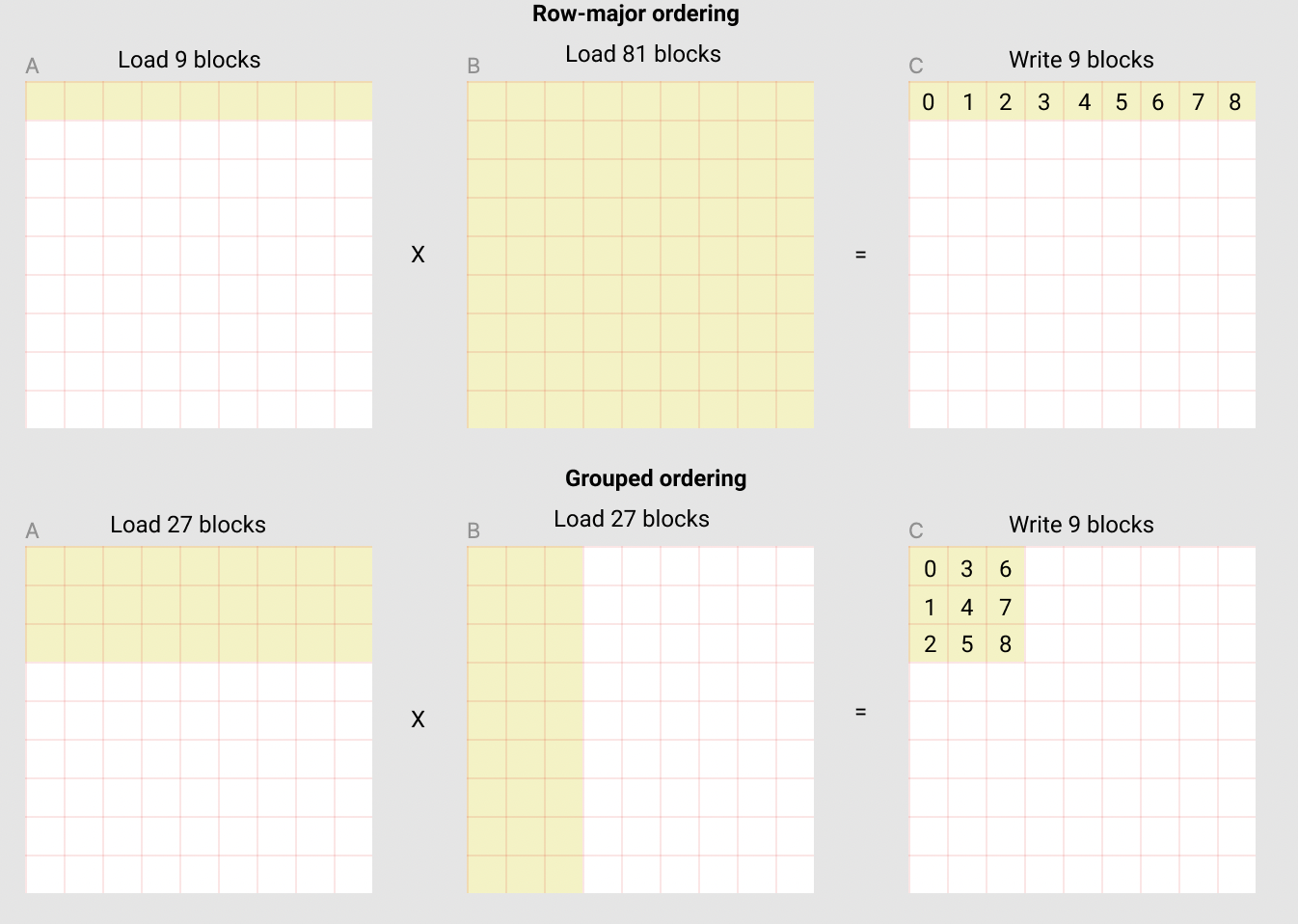
这个过程涉及到 pid 的重映射, 映射的方法如下:
pid = tl.program_id(0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M) # total number of blocks along M
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N) # total number of blocks along N
num_pid_in_group = GROUP_SIZE_M * num_pid_n # total number of blocks in a group
group_id = pid // num_pid_in_group # which group this pid belongs to
first_pid_m = group_id * GROUP_SIZE_M # first pid_m in this group
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M) # for the last group, may be smaller than GROUP_SIZE_M
pid_m = first_pid_m + (pid % num_pid_in_group)
pid_n = (pid % num_pid_in_group) // group_size_m # in column major order完整的矩阵乘法内核代码如下:
import triton
import triton.language as tl
@triton.jit
def matmul_kernel(
a_ptr, b_ptr, c_ptr,
M, N, K,
stride_am, stride_ak,
stride_bk, stride_bn,
stride_cm, stride_cn,
BLOCK_SIZE_M: tl.constexpr,
BLOCK_SIZE_N: tl.constexpr,
BLOCK_SIZE_K: tl.constexpr,
GROUP_SIZE_M: tl.constexpr
):
pid = tl.program_id(0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M) # total number of blocks along M
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N) # total number of blocks along N
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + (pid % num_pid_in_group)
pid_n = (pid % num_pid_in_group) // group_size_m
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
acc = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
a = tl.load(a_ptrs, mask=(offs_am[:, None] < M) & (offs_k[None, :] < K), other=0.0)
b = tl.load(b_ptrs, mask=(offs_k[:, None] < K) & (offs_bn[None, :] < N), other=0.0)
acc = tl.dot(a, b, acc=acc)
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
c = acc.to(tl.float16)
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + (offs_cm[:, None] * stride_cm + offs_cn[None, :] * stride_cn)
tl.store(c_ptrs, c, mask=(offs_cm[:, None] < M) & (offs_cn[None, :] < N))借矩阵乘的例子顺便演示一下 triton.autotune 的用法, 它可以用来自动调优内核参数, 例如 Block Size 和 Group Size 等等, 下面是一个例子
def get_autotune_config():
sizes = [
{ 'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 4 },
{ 'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 2 },
{ 'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 4 },
{ 'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 2 },
]
return [triton.Config(s, num_warps=4, num_stages=2) for s in sizes]
@triton.autotune(
configs=get_autotune_config(),
key=['M', 'N', 'K']
)
@triton.jit
def matmul_kernel( ..., M, N, K, ...):
...这里枚举了一些可能的参数组合 (生成一组列表), 然后传给 triton.autotune 装饰器, 并指定了调优的关键字参数 key. Triton 会根据传入的 key 参数值来选择最合适的配置进行编译和运行.